Find the equation of the plane passing through the line of intersection of the planes x + 2y + 3z – 5 = 0 and 3x - 2y –z + 1 = 0 and cutting off equal intercepts on the x-axis and z-axis.

Question

Philoid · Accepted Answer

Equation of plane through the line of intersection of planes in Cartesian form is

(1)

For the standard equation of planes in Cartesian form

So, putting in equation 1 we have

x + 2y + 3 z-5 + λ(3x -2y -z + 1)=0

(1 + 3λ)x + (2-2λ)y + (3-λ)z-5 + λ=0

Now equation of plane in intercept form

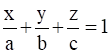
As given equal intercept means a=c

First, we transform equation of a plane in intercept form

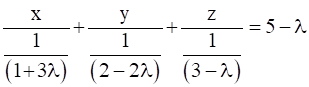
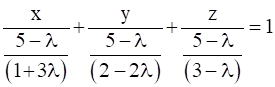
On comparing with the standard equation of a plane in intercept form

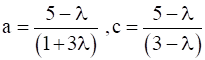
Now as a=b=c

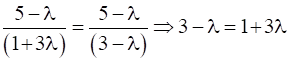
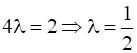
Putting in equation (2), we have

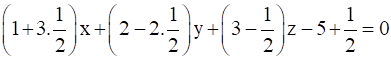
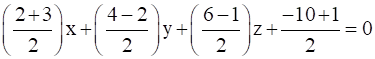
5x + 2y + 5z-9=0

5x + 2y + 5z=9

So, required equation of plane is 5x + 2y + 5z=9.