Given : Two cards are drawn from a well-shuffled pack of 52 cards.

To find : probability distribution of the number of kings and variance (σ²)

Formula used :

Mean = E(X) =

Variance = E(X²) -

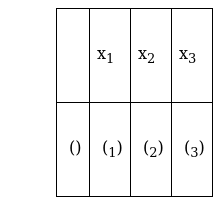
Mean = E(X) = = x₁P(x₁) + x₂P(x₂) + x₃P(x₃)

Two cards are drawn from a well-shuffled pack of 52 cards.

Let X denote the number of kings in the two cards

There are 4 king cards present in a pack of well-shuffled pack of 52 cards.

P(0) = = =

P(1) = = =

P(2) = = =

The probability distribution table is as follows,

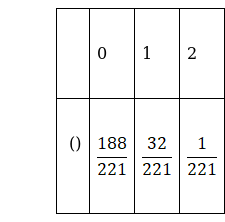
Mean = E(X) = 0() + 1() +2() = 0 + + = =

Mean = E(X) =

= =

E(X²) = = P(x₁) + P(x₂) + P(x₃)

E(X²) = () + () + () = 0 + + =

E(X²) =

Variance = E(X²) - = – = = =

Variance = E(X²) - =

The probability distribution table is as follows,

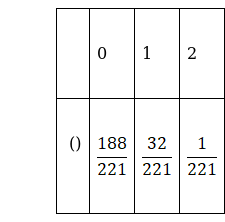
Variance =