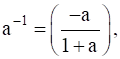(i) * is an operation as a*b = a+ b+ ab where a, b ∈ Q- {-1}. Let and two rational numbers.

So, * is a binary operation from - {-1}.

(ii) For commutative binary operation, a*b = b*a.

Since a*b = b*a, hence * is a commutative binary operation.

(iii) For associative binary operation, a*(b*c) = (a*b) *c

a+(b*c) = a*(b+ c+ bc) = a+ (b+ c+ bc) +a(b+ c+ bc)

= a+ b+ c+ bc+ ab+ ac+ abc

(a*b) *c = (a+ b+ ab) *c = a+ b+ ab+ c+ (a+ b+ ab) c

= a+ b+ c+ ab+ ac+ bc+ abc

Now as a*(b*c) = (a*b) *c, hence an associative binary operation.

(iv) For a binary operation *, e identity element exists if a*e = e*a = a. As a*b = a+ b- ab

a*e = a+ e+ ae (1)

e*a = e+ a +e a (2)

using a*e = a

a+ e+ ae = a

e+ ae = 0

e(1+a) = 0

either e = 0 or a = -1 as operation is on Q excluding -1 so a≠-1, hence e = 0.

So identity element e = 0.

(v) for a binary operation * if e is identity element then it is invertible with respect to * if for an element b, a*b = e = b*a where b is called inverse of * and denoted by a^-1.

a*b = 0

a+ b+ ab = 0

b(1+a) = -a