(i) A is said to be closed on * if all the elements of a*b ∈A. composition table is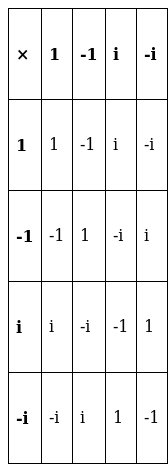

(as i² = -1)

As table contains all elements from set A, A is close for multiplication operation.

(ii) For associative, a× (b× c) = (a× b) ×c

1× (-i× i) = 1×1 = 1

(1× -i) ×i = -i× i = 1

a× (b× c) = (a× b) ×c, so A is associative for multiplication.

(iii) For commutative, a× b = b× a

1× -1 = -1

-1× 1 = -1

a× b = b× a, so A is commutative for multiplication.

(iv) For multiplicative identity element e, a× e = e× a = a where a ∈A.

a× e = a

a(e-1) = 0

either a = 0 or e = 1 as a≠0 hence e = 1.

So, multiplicative identity element e = 1.

(v) For multiplicative inverse of every element of A, a*b = e where a, b∈A.

1×b₁ = 1

b₁ = 1

-1×b₂ = 1

b₂ = -1

i×b₃ = 1

-i×b_{4 = 1}

So, multiplicative inverse of A = {1, -1, -i, i}