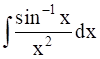
Tip – If f₁(x) and f₂(x) are two functions , then an integral of the form can be INTEGRATED BY PARTS as

where f₁(x) and f₂(x) are the first and second functions respectively.

Taking f₁(x) = sin^-1x and f₂(x) = 1/x²,

Taking x= sina, dx = cosada

Hence, coseca=1/x

Now, cosec²a-cot²a = 1 so cota=√(1-x²)/x

Replacing the value of a, we get,

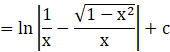
The total integration yields as

, where c is the integrating constant