Find the Cartesian and vector equations of a plane passing through the point (1, 2, - 4) and parallel to the lines 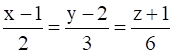 and
and 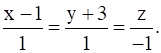
Given - ![]() &
& ![]() . A plane is parallel to both these lines and passes through (1, 2, - 4).
. A plane is parallel to both these lines and passes through (1, 2, - 4).
To find – The equation of the plane
Tip – A plane parallel to two vectors will have its normal in a direction perpendicular to both the vectors, which can be evaluated by taking their cross product
The direction ratios of the given lines are (2, 3, 6) and (1, 1, - 1)
![]() &
& ![]()
![]()
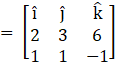
![]()
![]()
The equation of the plane maybe represented as - 9x + 8y - z + d = 0
Now, this plane passes through the point (1, 2, - 4)
Hence,
(- 9) × 1 + 8 × 2 - (- 4) + d = 0
⇒ d = - 11
The Cartesian equation of the plane : - 9x + 8y - z - 11 = 0 i.e. 9x - 8y + z + 11 = 0
The vector equation : ![]()
1