Find the particular solution of the differential equation xe y/x - y + x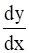 = 0, given that y(e) = 0.

Question

Philoid · Accepted Answer

⇒ the given differential equation is a homogenous equation.

The solution of the given differential equation is :

Put y = vx

Integrating both the sides we get:

Resubstituting the value of y = vx we get

Now,y(e) = 0

y = - xlog(log|x|)

Ans: y = - xlog(log|x|)