Solve Given Equation: Re-arranging, we get, Let 2 – ey = t -eydy = dt Therefore, Integrating both sides, we get, log t = log(x + 1) + C log (2 – ey) = log (x + 1) + C At x = 0, y = 0. Therefore, log(2) = log(1) + C Therefore, C = log 2 Now, we have, log (2 – ey) – log (x + 1) – log 2 = 0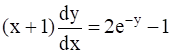 , given that
, given that 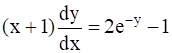
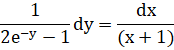
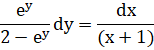
![]()
![]()
1