Find the shortest distance between the lines given below:
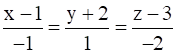 and
and 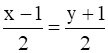
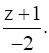
Given : Cartesian equations of lines
![]()
![]()
To Find : distance d
Formulae :
1. Equation of line :
Equation of line passing through point A (a1, a2, a3) and having direction ratios (b1, b2, b3) is
![]()
Where, ![]()
And ![]()
2. Cross Product :
If ![]() are two vectors
are two vectors
![]()
![]()
then,
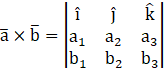
3. Dot Product :
If ![]() are two vectors
are two vectors
![]()
![]()
then,
![]()
4. Shortest distance between two lines :
The shortest distance between the skew lines ![]() and
and
![]() is given by,
is given by,
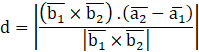
Answer :
Given Cartesian equations of lines
![]()
Line L1 is passing through point (1, -2, 3) and has direction ratios (-1, 1, -2)
Therefore, vector equation of line L1 is
![]()
And
![]()
Line L2 is passing through point (1, -1, -1) and has direction ratios (2, 2, -2)
Therefore, vector equation of line L2 is
![]()
Now, to calculate distance between the lines,
![]()
![]()
Here,
![]()
![]()
![]()
![]()
Therefore,
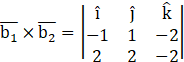
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Now,
![]()
![]()
= 0 - 6 + 16
= 10
Therefore, the shortest distance between the given lines is
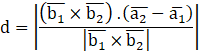
![]()
![]()
![]()