Find the length and the equations of the line of shortest distance between the lines given by:
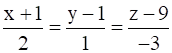 and
and 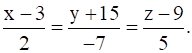
Given : Cartesian equations of lines
![]()
![]()
Formulae :
1. Condition for perpendicularity :
If line L1 has direction ratios (a1, a2, a3) and that of line L2 are (b1, b2, b3) then lines L1 and L2 will be perpendicular to each other if
![]()
2. Distance formula :
Distance between two points A≡(a1, a2, a3) and B≡(b1, b2, b3) is given by,
![]()
3. Equation of line :
Equation of line passing through points A≡(x1, y1, z1) and B≡(x2, y2, z2) is given by,
![]()
Answer :
Given equations of lines
![]()
![]()
Direction ratios of L1 and L2 are (2, 1, -3) and (2, -7, 5) respectively.
Let, general point on line L1 is P≡(x1, y1, z1)
x1 = 2s-1 , y1 = s+1 , z1 = -3s+9
and let, general point on line L2 is Q≡(x2, y2, z2)
x2 = 2t+3 , y2 = -7t – 15 , z2 = 5t + 9
![]()
![]()
![]()
Direction ratios of ![]() are ((5t - 2s + 10), (-7t – s – 16), (5t + 3s))
are ((5t - 2s + 10), (-7t – s – 16), (5t + 3s))
PQ will be the shortest distance if it perpendicular to both the given lines
Therefore, by the condition of perpendicularity,
2(5t - 2s + 10) + 1(-7t – s – 16) - 3(5t + 3s) = 0 and
2(5t - 2s + 10) – 7(-7t – s – 16) + 5(5t + 3s) = 0
⇒ 10t – 4s + 20 - 7t – s - 16 - 15t – 9s = 0 and
10t - 4s + 20 + 49t + 7s + 112 + 25t + 15s = 0
⇒ -12t – 14s = -4 and
84t + 18s = -132
Solving above two equations, we get,
t = -2 and s = 2
therefore,
P ≡ (3, 3, 3) and Q ≡ (-1, -1, -1)
Now, distance between points P and Q is
![]()
![]()
![]()
![]()
![]()
Therefore, the shortest distance between two given lines is
![]()
Now, equation of line passing through points P and Q is,
![]()
![]()
![]()
![]()
⇒ ![]()
Therefore, equation of line of shortest distance between two given lines is
x = y = z