Given:

Rate of working of an engine R, v is the speed of the engine:

, where 0<v<30

For finding the maximum/ minimum of given function, we can find it by differentiating it with v and then equating it to zero. This is because if the function f(x) has a maximum/minimum at a point c then f’(c) = 0.

Now, differentiating the function R with respect to v.

----- (1)

[Since and ]

Equating equation (1) to zero to find the critical value.

v² = 400

v = 20 (or) v = -20

As given in the question 0<v<30, v = 20

Now, for checking if the value of R is maximum or minimum at v=20, we will perform the second differentiation and check the value of at the critical value v = 20.

Differentiating Equation (1) with respect to v again:

[Since and ]

----- (2)

Now find the value of

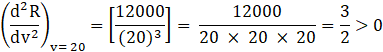
So, at critical point v = 20. The function R is at its minimum.

Hence, the function R is at its minimum at v = 20.