Given,

• Rectangle with given perimeter.

Let us consider,

• ‘p’ as the fixed perimeter of the rectangle.

• ‘x’ and ‘y’ be the sides of the given rectangle.

• Area of the rectangle, A = x × y.

Now as consider the perimeter of the rectangle,

p = 2(x +y)

p = 2x + 2y

----- (1)

Consider the area of the rectangle,

A = x × y

Substituting (1) in the area of the rectangle,

----- (2)

For finding the maximum/ minimum of given function, we can find it by differentiating it with x and then equating it to zero. This is because if the function f(x) has a maximum/minimum at a point c then f’(c) = 0.

Differentiating the equation (2) with respect to x:

[Since ]

----- (3)

To find the critical point, we need to equate equation (3) to zero.

Now to check if this critical point will determine the largest rectangle, we need to check with second differential which needs to be negative.

Consider differentiating the equation (3) with x:

[Since and ]

------ (4)

Now, consider the value of

As , so the function P is maximum at .

Now substituting in equation (1):

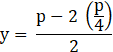
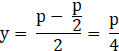
As the sides of the taken rectangle are equal, we can clearly say that a largest rectangle which has a given perimeter is a square.