Given,

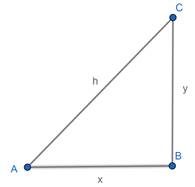
• A right angle triangle.

• Hypotenuse of the given triangle is given.

Let us consider,

• ‘h’ is the hypotenuse of the given triangle.

• ‘x’ and ‘y’ be the base and height of the right angle triangle.

• The hypotenuse of the ΔABC = AC² = AB² + BC²

AC = h, AB = x and BC = y

Hence,

h² = x² + y²

y² = h² – x²

--- (1)

Now, perimeter of the ΔABC is

P = h + x + y

Now substituting (1) in the area of the triangle,

----- (2)

For finding the maximum/ minimum of given function, we can find it by differentiating it with x and then equating it to zero. This is because if the function f(x) has a maximum/minimum at a point c then f’(c) = 0.

Differentiating the equation (2) with respect to x:

[Since ]

------ (3)

To find the critical point, we need to equate equation (3) to zero.

[squaring on both sides]

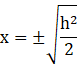
[as the base of the triangle cannot be negative.]

Now to check if this critical point will determine the maximum perimeter of the triangle, we need to check with second differential which needs to be negative.

Consider differentiating the equation (3) with x:

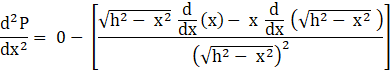
[Since if u and v are two functions of x, then ]

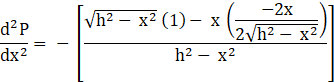
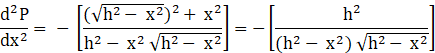
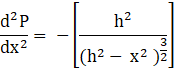
Now, consider the value of

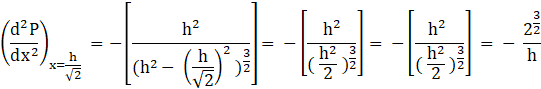
As , so the function A is maximum at .

Now substituting in equation (1):

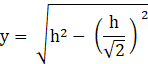
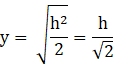
As , the base and height of the triangle are equal, which means that two sides of a right angled triangle are equal,

Hence the given triangle is an isosceles triangle with sides AB and BC equal.