Prove that the volume of the largest cone that can be inscribed in a sphere is  of the volume of the sphere.
of the volume of the sphere.
Given,
• Volume of the sphere.
• Volume of the cone.
• Cone is inscribed in the sphere.
• Volume of cone is maximum.
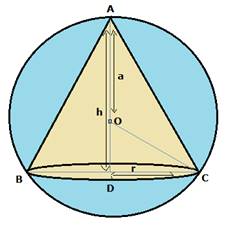
Let us consider,
• The radius of the sphere be ‘a’ units.
• Volume of the inscribed cone be ‘V’.
• Height of the inscribed cone be ‘h’.
• Radius of the base of the cone is ‘r’.
Given volume of the inscribed cone is,
![]()
Consider OD = (AD-OA) =(h-a)
Now let OC2 = OD2 + DC2, here OC = a, OD = (h-a), DC = r,
So a2 = (h-a)2 + r2
r2 = a2 – (h2+ a2 – 2ah)
r2 = h (2a -h) ----- (1)
Let us consider the volume of the cone:
![]()
Now substituting (1) in the volume formula,
![]()
![]() ---- (2)
---- (2)
For finding the maximum/ minimum of given function, we can find it by differentiating it with h and then equating it to zero. This is because if the function V(r) has a maximum/minimum at a point c then V’(c) = 0.
Differentiating the equation (2) with respect to h:
![]()
![]()
[Since ![]() ]
]
![]() ------- (3)
------- (3)
To find the critical point, we need to equate equation (3) to zero.
![]()
4πah – 3πh2 = 0
h(4πa-3πh)= 0
h = 0 (or) ![]()
![]()
[as h cannot be zero]
Now to check if this critical point will determine the maximum volume of the inscribed cone, we need to check with second differential which needs to be negative.
Consider differentiating the equation (3) with h:
![]()
![]() ----- (4)
----- (4)
[Since ![]() ]
]
Now let us find the value of

As ![]() , so the function V is maximum at
, so the function V is maximum at ![]()
Substituting h in equation (1)
![]()
![]()
![]()
As V is maximum, substituting h and r in the volume formula:
![]()
![]()
![]()
Therefore when the volume of a inscribed cone is maximum, then it is equal to ![]() times of the volume of the sphere in which it is inscribed.
times of the volume of the sphere in which it is inscribed.