Given,

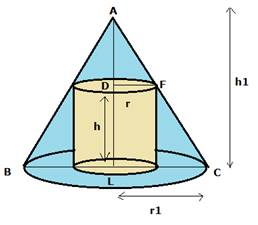
• A right circular cylinder is inscribed inside a cone.

• The curved surface area is maximum.

Let us consider,

• ‘r₁’ be the radius of the cone.

• ‘h₁’ be the height of the cone.

• ‘r’ be the radius of the inscribed cylinder.

• ‘h’ be the height of the inscribed cylinder.

DF = r, and AD = AL – DL = h₁ – h

Now, here ΔADF and ΔALC are similar,

Then

----- (1)

Now let us consider the curved surface area of the cylinder,

S = 2πrh

Substituting h in the formula,

---- (2)

For finding the maximum/ minimum of given function, we can find it by differentiating it with r and then equating it to zero. This is because if the function S(r) has a maximum/minimum at a point c then S’(c) = 0.

Differentiating the equation (2) with respect to r:

[Since ]

------- (3)

To find the critical point, we need to equate equation (3) to zero.

Now to check if this critical point will determine the maximum volume of the inscribed cylinder, we need to check with second differential which needs to be negative.

Consider differentiating the equation (3) with r:

----- (4)

[Since ]

Now let us find the value of

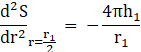
As , so the function S is maximum at

Substituting r in equation (1)

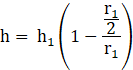
--- (5)

As S is maximum, from (5) we can clearly say that h₁ = 2h and

r₁ = 2r

this means the radius of the cone is twice the radius of the cylinder or equal to diameter of the cylinder.