Given the boundaries of the area to be found are,

• the circle, x² + y² = 25 ---(1)

• the parabola, y² = 8x ---- (2)

From the equation, of the first circle, x² + y² = 25

• the vertex at (0,0) i.e. the origin

• the radius is 5 units.

From the equation, of the parabola , y² = 8x

• the vertex at (0,0) i.e. the origin

• Symmetric about the x-axis, as it has the even power of y.

Now to find the point of intersection of (1) and (2), substitute y² = 8x in (1)

x² + 8x = 25

x² + 8x - 25= 0

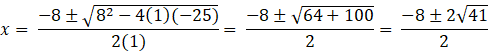
as y cannot be imaginary, we reject the negative value of x

so

So the two points, A and B are the points where (1) and (2) meet.

The line AB meets the x-axis at D = [(√41 -4),0]

Substitute y = 0 in (1),

x² + 0 = 25

x = ±5

So the circle intersects the x-axis at C(5,0)and E(-5,0)

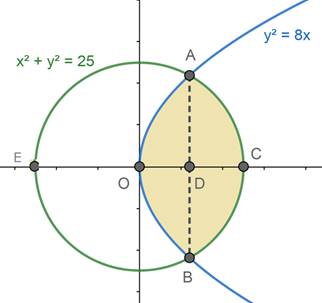
As x and y have even powers for the circle, they will be symmetrical about the x-axis and y-axis.

Consider the circle, x² + y² = 25, can be re-written as

----- (3)

Consider the parabola, y² = 8x, can be re-written as

----- (4)

Now, the area to be found will be the area is

Area of the required region = Area of OACBO.

Area of OABCO= Area of OCAO+ Area of OCBO

[area of OCBO= area of OCAOas the circle is symmetrical about the y-axis]

Area of OACBO= 2 × Area of OCAO---- (5)

Area of OCAO= Area of OADO+ Area of DACD

Area of OCAOis

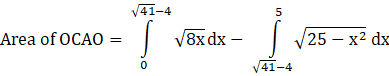
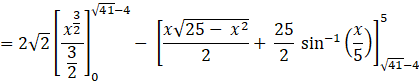
[Using the formula, and ]

Let √41 – 4 = a

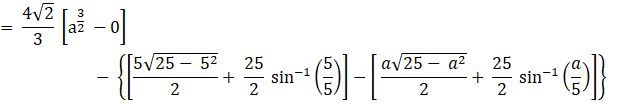
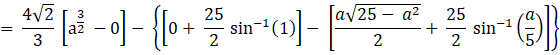
[sin^-1(1) = 90° and sin^-1(0) = 0°]

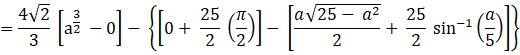
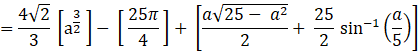
The Area of OCAOsq. units, where a = √41 - 4

Now substituting the area of OCAOin equation (5)

Area of OACBO= 2 × Area of OCAO

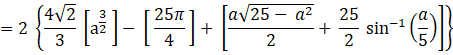
Area of the required region is sq. units, where a = √41 - 4