Draw a rough sketch of the region ![]() and find the area enclosed by the region, using the method of integration.
and find the area enclosed by the region, using the method of integration.
Given the boundaries of the area to be found are,
R = {(x,y): y2 ≤ 3x, 3x2 + 3y2 ≤ 16}
This can be written as
R1 = {(x,y): y2 ≤ 3x}
R2 = {(x,y): 3x2 + 3y2 ≤ 16}
Then ![]()
From R1, we can say that , y2 = 3x is a parabola
y2 = 3x ---- (1)
• With vertex at (0,0) i.e. the origin
• Symmetric about the x-axis, as it has the even power of y
From R1, we can say that , 3x2 + 3y2 = 16 is a circle
3x2 + 3y2 = 16 ----- (2)
• the vertex at (0,0) i.e. the origin
• the radius of ![]() units
units
Now to find the point of intersection of (1) and (2), substitute y2 = 3x in (2)
3x2 + 3(3x) = 16
3x2 + 9x - 16= 0
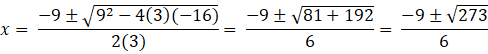
as y cannot be imaginary, we reject the negative value of x
so ![]()
So the two points, A and B are the points where (1) and (2) meet.
The line AB meets the x-axis at ![]()
Substitute y = 0 in (2),
3x2 + 0 = 16
![]()
So the circle intersects the x-axis at ![]() and
and ![]()
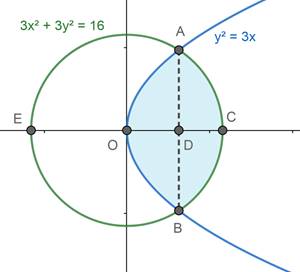
As x and y have even powers for the circle, they will be symmetrical about the x-axis and y-axis.
Consider the circle, 3x2 + 3y2 = 16, can be re-written as
![]()
![]() ----- (3)
----- (3)
Consider the parabola, y2 = 3x, can be re-written as
![]() ----- (4)
----- (4)
Now, the area to be found will be the area is
Area of the required region = Area of OACBO.
Area of OABCO= Area of OCAO+ Area of OCBO
[area of OCBO= area of OCAOas the circle is symmetrical about the y-axis]
Area of OACBO= 2 × Area of OCAO---- (5)
Area of OCAO= Area of OADO+ Area of DACD
Area of OCAOis
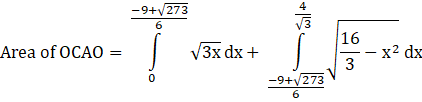
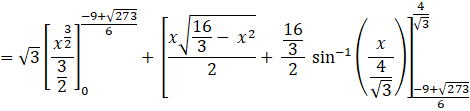
[Using the formula, ![]() and
and ![]() ]
]
Let ![]()
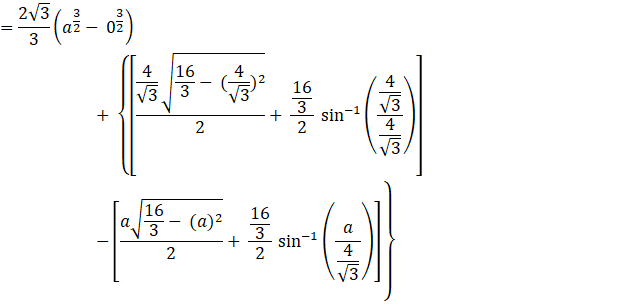

[sin-1(1) = 90° and sin-1(0) = 0°]
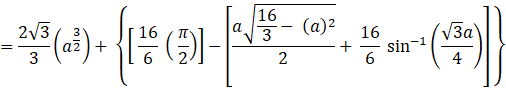
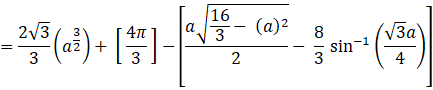
The Area of OCAO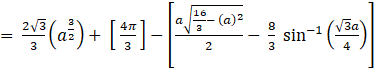 sq. units, where
sq. units, where ![]()
Now substituting the area of OCAOin equation (5)
Area of OACBO= 2 × Area of OCAO
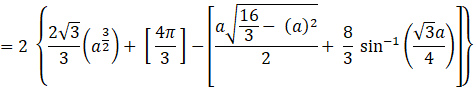
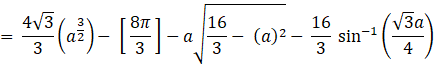
Area of the required region is ![]() sq. units, where
sq. units, where ![]()