Given : Equations of lines -

To Prove : are coplanar.

To Find : Equation of plane.

Formulae :

1) Cross Product :

If are two vectors

then,

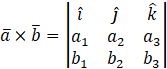
2) Dot Product :

If are two vectors

then,

3) Coplanarity of two lines :

If two lines are coplanar then

4) Equation of plane :

If two lines are coplanar then equation of the plane containing them is

Where,

Answer :

Given equations of lines are

Let,

Where,

Now,

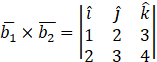
Therefore,

= 0 + 4 + 3

= 7

……… eq(1)

And

= - 2 + 12 – 3

= 7

……… eq(2)

From eq(1) and eq(2)

Hence lines are coplanar.

Equation of plane containing lines is

Now,

From eq(1)

Therefore, equation of required plane is