Prove that the lines 
and 
are coplanar. Also find the equation of the plane containing these lines.
Given : Equations of lines –
Line 1 : 
Line 2 : 
To Prove : Line 1 & line 2 are coplanar.
To Find : Equation of plane.
Formulae :
1) Coplanarity of two lines :
If two lines are given by,
and
, then these lines are coplanar, if
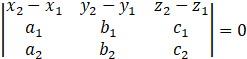
2) Equation of plane :
The equation of plane containing two coplanar lines 
& 
is given by,
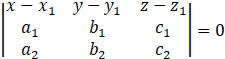
Answer :
Given lines –
Line 1 : 
Line 2 : 
Here, x1 = 2 , y1 = 4 , z1 = 6 , a1 = 1 , b1 = 4 , c1 = 7
x2 = -1 , y2 = -3 , z2 = -5 , a2 = 3 , b2 = 5 , c2 = 7
Now,
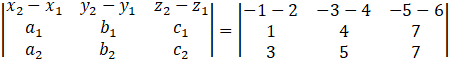
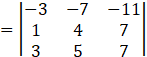
= 21 - 98 + 77
= 0
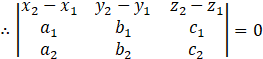
Hence, given two lines are coplanar.
Equation of plane passing through line 1 and line 2 is given by,
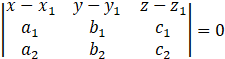
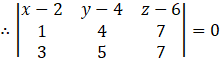
-7x + 14 + 14y - 56 – 7z + 42 = 0
- 7x + 14y – 7z = 0
x – 2y + z = 0
Therefore, equation of plane is
x – 2y + z = 0