Show that the four points A(0, -1, 0),
B(2, 1, -1), C(1, 1, 1) and D(3, 3, 0) are coplanar. Find the equation of the plane containing them.
Given Points :
A = (0, -1, 0)
B = (2, 1, -1)
C = (1, 1, 1)
D = (3, 3, 0)
To Prove : Points A, B, C & D are coplanar.
To Find : Equation of plane passing through points A, B, C & D.
Formulae :
1) Position vectors :
If A is a point having co-ordinates (a1, a2, a3), then its position vector is given by,
2) Equation of line
If A and B are two points having position vectors 
then equation of line passing through two points is given by,
3) Cross Product :
If 
are two vectors
then,
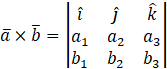
4) Dot Product :
If 
are two vectors
then,
5) Coplanarity of two lines :
If two lines 
are coplanar then
6) Equation of plane :
If two lines 
are coplanar then equation of the plane containing them is
Where,
For given points,
A = (0, -1, 0)
B = (2, 1, -1)
C = (1, 1, 1)
D = (3, 3, 0)
Position vectors are given by,
Equation of line passing through points A & D is
Let, 
Where,
& 
And equation of line passing through points B & C is
Let, 
Where,
& 
Now,
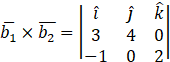
Therefore,
= 0 + 6 + 0
= 6
……… eq(1)
And
= 16 – 6 – 4
= 6
……… eq(2)
From eq(1) and eq(2)
Hence lines 
are coplanar
Therefore, points A, B, C & D are also coplanar.
As lines 
are coplanar therefore equation of the plane passing through two lines containing four given points is
Now,
= 8x - 6y + 4z
From eq(1)
Therefore, equation of required plane is
8x - 6y + 4z = 6
4x - 3y + 2z = 3