Given :

Equation of plane :

A = (1, 1, 2)

To Find :

i) Length of perpendicular = d

ii) coordinates of the foot of the perpendicular

Formulae :

1) Unit Vector :

Let be any vector

Then unit vector of is

Where,

2) Length of perpendicular :

The length of the perpendicular from point A with position vector to the plane is given by,

Note :

If two vectors with direction ratios (a₁, a₂, a₃) & (b₁, b₂, b₃) are parallel then

Given equation of the plane is

………..eq(1)

As

Therefore equation of plane is

2x – 2y + 4z = -5 ……… eq(2)

From eq(1) normal vector of the plane is

From eq(1), p = -5

Given point A = (1, 1, 2)

Position vector of A is

Now,

= (1×2) + (1×(-2)) + (2×4)

= 2 – 2 + 8

= 8

Length of the perpendicular from point A to the plane is

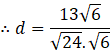
Let P be the foot of perpendicular drawn from point A to the given plane,

Let P = (x, y, z)

As normal vector and are parallel

⇒x = 2k+1, y = -2k+1, z = 4k+2

As point P lies on the plane, we can write

2(2k+1) – 2(-2k+1) + 4(4k+2) = -5

⇒ 4k + 2 + 4k – 2 + 16k + 8 = -5

⇒ 24k = -13

,

Therefore co-ordinates of the foot of perpendicular are

P(x, y, z) =

P ≡