A small firm manufactures necklace and bracelets. The total number of necklace and bracelet that it can handle per day is at most 24. It takes 1 hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is ₹100 and that on a bracelet is ₹300, how many of each should be produced daily to maximize the profit? It is being given that at least one of each must be produced.
Let the firm manufacture x number of necklaces and y number of bracelets a day.
∴According to the question,
X + y
, 0.5x + y 
x
Maximize Z = 100x + 300y
The feasible region determined by X + y
, 0.5x + y 
x
is given by
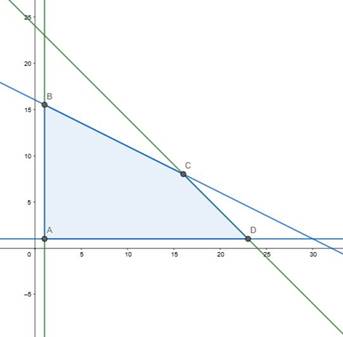
The corner points of the feasible region are A(1,1) , B(1,15.5) , C(16,8) , D(23,1).The number of bracelets should be whole number. Therefore, considering point (2,15). The value of Z at corner point is
The maximum value of Z is 4700 at point B(2,15).
∴ The firm should make 2 necklaces and 15 bracelets.