Figure shows graphs of pressure vs density for an ideal gas at two temperatures T1 and T2.
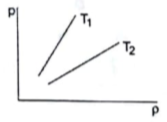
From the graph, we can see that slope of straight line with temperature
T1 is greater than slope of straight line with temperature T2.
Slope of straight line is given as:
Slope =![]()
In our graph, slope is ![]()
where P=pressure
![]() = density of gas
= density of gas
So, ratio ![]() for T1 is more than T2.
for T1 is more than T2.
Rms speed of gas is given as
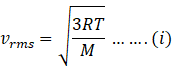
where R=gas constant whose value is 8.31 J/mol K.
T=temperature of gas.
M= molar mass of molecule of gas
We also know that ideal gas equation is
PV=nRT
Where V= volume of gas
R=gas constant
T=temperature
N=number of moles of gas
So, we can write ![]() .
.
Putting the value of RT in equation (i),we get
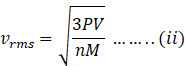
nM= total mass of gas ‘m’
and density ![]() =
=![]()
Putting the value of density ![]() in equation (ii), we get
in equation (ii), we get
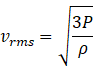
Since ratio ![]() for T1 is more than T2 therefore rms speed for ideal gas at temperature T1 is more than temperature T2. And if rms speed is more for temperature T1 then T1 > T2 from formula
for T1 is more than T2 therefore rms speed for ideal gas at temperature T1 is more than temperature T2. And if rms speed is more for temperature T1 then T1 > T2 from formula
vrms =![]()