Hydrogen gas is contained in a closed vessel at 1 atm (100 kPa) and 300 K

(a) Calculate the means speed of the molecules.


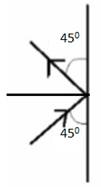
(b) Suppose the molecules strike the wall with this speed making an average angle of 45° with it.


How many molecules strike each square meter of the wall per second?


(a)

In kinetic theory of ideal gas, mean speed also known as average speed is given as



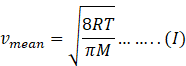
Where R=gas constant=8.31Jmol-1K-1


T=temperature of gas


M=molar mass of gas


Given


T=300k


Molar mass of hydrogen gas =2amu=2g/mol=2kg/mol



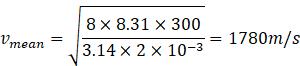
(b)



Let velocity be u= from part (a)


From figure we can see that


Total Momentum in vertical direction


mucos45-mucos45=0


Total momentum in horizontal direction


musin45-(-musin45)=2musin45=2mumu


Total change momentum of 1 molecules =mu


Total change momentum of n molecules =nmu


We know that,



Let ‘t’ be the time taken to changing the momentum.


So, force per unit second due to 1 molecule=mu


Force per unit second due to n molecule=nmu


Given


Pressure by n molecule=105 Pa


Area=1m2


Pressure =




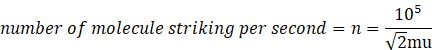
We know that


Mass of 6.023 of hydrogen molecule=2kg


Mass of 1 hydrogen molecule m =kg


Therefore



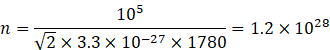
Number of molecules strike each square meter of the wall per second=1.2


1