Air is pumped into the tubes of a cycle rickshaw at a pressure of 2 atm. The volume of each tube at this pressure is 0.002 m3. One of the tubes gets punctured and the volume of the tube reduces to 0.0005 m3. How many moles of air have leaked out? Assume that the temperature remains constant at 300K and that the air behaves as an ideal gas.
We know ideal gas equation
PV=nRT
Where V= volume of gas
R=gas constant=8.31Jmol-1K-1
T=temperature
n=number of moles of gas
P=pressure of gas
Given
Pressure inside the tyre P1=2atm=2![]() Pa
Pa
Volume at P1, V1=0.002m3
Reduced volume V2=0.0005m3
Temperature remains constant so T1=T2=300K
Let when the gas is leaked out the pressure P2 becomes equal to atmospheric pressure. So P2=1.0![]() Pa.
Pa.
Number of moles initially n1
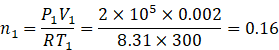
Similarly
Final number of moles n2
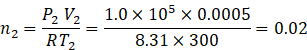
So, number of moles leaked out will be n1-n2=0.16-0.02=0.14.