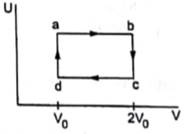
Figure shows the variation in the internal energy U with the volume V of 2.0 mol of an ideal gas in a cyclic process abcda. The temperatures of the gas at b and c are 500 K and 300 K respectively. Calculate the heat absorbed by the gas during the process.
Given
Number of moles n=2
Temperature at b Tb=500K
Temperature at c Tc=300K
From the graph it is clear that
Tb=Ta and Td=Tc
Thus, path ab and cd are isothermal paths.
We know that work done by the gas is given as
ΔW=PΔV
Where ΔV =change in volume
P =pressure
Again, from the graph we can see that ΔV=0 for path bc and da.
Therefore, work done along path bc and da are zero.
So, total work done ΔW=Wab+Wcd
We know that work done in an isothermal process is given as
![]()
Where n=number of moles
R=gas constant =8.31J/Kmol
T=temperature
Vf=final volume
Vi=initial volume
![]()
![]()
Wab = 8310×ln2
Similarly,
![]()
![]()
![]()
Wcd = -4986 ×ln2
So, total work done ΔW=Wab+Wcd
=8310×ln2 - 4986×ln2
=3324×ln2
ΔW =3324×0.693=2304.02J
From first law of thermodynamics, we know that,
ΔQ=ΔU+ΔW
Where ΔQ=heat supplied to the system
ΔU=change in internal energy
ΔW=work done by the system
Process ABCA is a cyclic process. The system is brought back to its initial state. Since internal energy is a state function, change in internal energy will be zero.
So, ΔU=0.
So, first law becomes
ΔQ=ΔW=2304.02J
Thus, heat absorbed by the system is 2304.02J.