Seven rods A, B, C, D, E, F and G are joined as shown in figure. All the rods have equal cross-sectional area A and length ℓ. The thermal conductivities of the rods are KA = KC = KD, KD = 2KD, KE = 3KD, KF = 4KD and KD = 5KD. The rod E is kept at a constant temperature T1 and the rod G is kept at a constant temperature T2(T2> T1).
(a) Show that the rod F ahs a uniform temperature T = (T1 + 2T2)/3.
(b) Find the rate of heat flowing from the source which maintains the temperature T2.
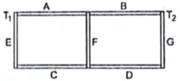
Given thermal conductivity of the respective rods as follows-
KA = KC = K0
KB = KD = 2K0
KE = 3K0, KF = 4K0
K9= 5K0
Also, length of each rod is l
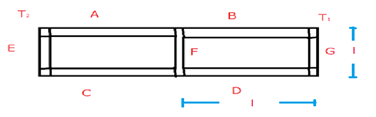
At steady state, temperature at the ends of rod F will be same.
Let T be the temperature of rod F
(a)
Rate of heat flow through rod A + rod C
= Rate of heat flow through rod B + rod D
![]()
⇒ ![]() +
+![]() =
= ![]() +
+![]()
Substituting the values in terms of k0 –
⇒ ![]() +
+![]() =
= ![]() +
+![]()
⇒ 2k0 (T1-T) = 2 ![]() 2 k0 (T–T2)
2 k0 (T–T2)
⇒ T = ![]()
(b) To find the rate of flow of heat from rod G, which is at Temperature T2
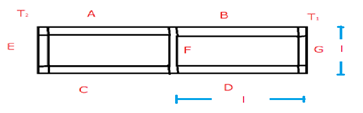
Looking into the above diagram, we can say that it forms a balanced Wheatstone bridge.
Also, as the ends of rod F are maintained at the same temperature, no heat current flows through rod F.
Hence we can remove the F for simplification
From above diagram, we can see that RA and RB are connected in series.
⇒ RAB = RA + RB
And RC and RD are connected in series
⇒ RCD = RC + RD
Then, RAB and RCD are connected in parallel
Now ,
RA = ![]() , RB =
, RB = ![]() , RC =
, RC = ![]() , RD =
, RD = ![]()
Since RA , RB are connected in series
RAB = ![]() and RCD =
and RCD = ![]()
Since RAB RCD are in parallel
![]() =
= ![]()
= ![]()
= ![]()
Now, rate of flow of heat from the source rod
q = ![]() =
= ![]()
=![]()
Hence, rate of flow of heat from the source rod is given by
q = ![]()