Two unequal resistances R 1 and R 2 are connected across two identical batteries of emf ϵ and internal resistance r. Can the thermal energies developed in R 1 and R 2 be equal in a given time. If yes, what will be the condition ?

Question

Philoid · Accepted Answer

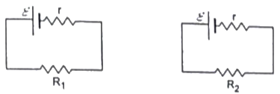
Given ∈ as emfs of the circuits with internal resistances r

Let the currents passing through the

resistance R₁ and R₂ be i₁ and i₂ , respectively for time t.

According to Kirchhoff’s Voltage Law, sum of

all voltages around any closed loop in a

circuit must equal zero.

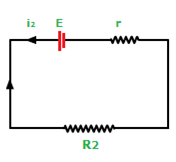
ie,

Looking into the circuit 1-we get-

(1)

Similarly, the current in the other circuit,

(2)

The heat lost through a resistor r is given by

(3)

Now the total thermal energies through the resistances from Joule’s heating effect are given

by -

=

From(1), (2) and (3)

⇒( = (

Hence, the condition when the thermal energies developed in

R₁and R₂ be equal in a given time is when the internal resistance r–

Two unequal resistances R1 and R2 are connected across two identical batteries of emf ϵ and internal resistance r. Can the thermal energies developed in R1 and R2 be equal in a given time. If yes, what will be the condition?

Two unequal resistances R₁ and R₂ are connected across two identical batteries of emf ϵ and internal resistance r. Can the thermal energies developed in R₁ and R₂ be equal in a given time. If yes, what will be the condition?