we assume a sphere of radius r and light falls on it.

We assume a ring on it with breath rdθ (as dθ is very small), dθ is the angle which forms with the center as origin and the breath of strip.

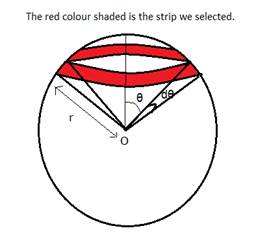
Area of strip =length × breath

Length =

Breath=

∴ It’s area is

∴ The energy falling on ring in dt time will be

dE=I dt da cosθ …. equation (1)

and the momentum it imparts will be

dp = from equation 1 of question 6 we have this formula.

Putting the value of dE from equation 1 in above equation,

Hence the force is

df =

Component of force onto the straight line which is passing through center of sphere and the origin of source.

=

Hence force on entire sphere, by applying proper limits of θ from 0 to π

Force =

=

=[put cosθ =t and solve by replacing it as and replacing limits 1 to 0]

=

i.e. this is same for above also.