HC Verma - Concepts of Physics Part 2

Book: HC Verma - Concepts of Physics Part 2

Chapter: 27. Specific Heat Capacities of Gases

Subject: Physics - Class 12th

Q. No. 6 of Objective I

Listen NCERT Audio Books - Kitabein Ab Bolengi

6

The molar heat capacity for the process shown in the figure is



Let us consider the figure given below :



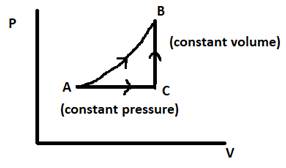
We consider the process AB to be composed of two processes, AC(at constant pressure) and CB(at constant volume), such that AB = AC + CB. C is the molar heat capacity of AB, Cp is the molar heat capacity of AC(constant pressure) and Cv is the molar heat capacity of CB(constant volume).


From the first law of thermodynamics, we know that Q = U + W … (i),


Where Q = heat supplied, U = change in internal energy, W = work done on the system.


Since the change in internal energy is independent of the path, it will have the same value for paths AB and ACB.


Hence, UAB = UACB … (ii), where UAB = change in internal energy for path AB, UACB = change in internal energy for path ACB.


Now, the work done by a process is given by the area under the PV diagram. We can clearly see that the area under process AB is greater than the sum of areas under processes AC and CB.


Hence, WAB > WACB … (iii), where WAB = work done for process following path AB, WACB = work done for process following path ACB.


Adding (ii) and (iii), we get :


UAB + WAB > UACB + WACB … (iv)


But, from the first law of thermodynamics, Q = U + W, where Q = heat supplied, U = change in internal energy, W = work done on the system.


Hence, we get, QAB > QACB … (v),


We know, QAB = nCdT, QAC = nCpdT, QCB = nCvdT,


where QAB = heat supplied in process AB


QAC = heat supplied in process AC


QCB = heat supplied in process CB


n = number of moles


C = molar heat capacity


Cp = molar heat capacity at constant pressure


Cv = molar heat capacity at constant volume


dT = change in temperature.


Also, QACB = QAC + QCB … (vi), where


QACB = heat supplied in process ACB


QAC = heat supplied in process AC


QCB = heat supplied in process CB


Hence, from (v), we get,


nCdT > nCpdT + nCvdT


Dividing by ndT on both sides :


C > Cp + Cv => C > Cv (option c)

1

Chapter Exercises

Short Answer
Objective I
Objective II
Exercises

More Exercise Questions

1

Work done by a sample of an ideal gas in a process A is double the work done in another process B. The temperature rises through the same amount in the two processes. If CA and CB be the molar heat capacities for the two processes.
2

For a solid with a small expansion coefficient,
3

The value of CP – CV is 1.00 R for a gas sample in state A and is 1.08R in state B. Let PA, PB denote the pressures and TA, and TB denote the temperatures of the states A and B respectively. Most likely
4

Let CV and CP denote the molar heat capacities of an ideal gas at constant volume and constant pressure respectively. Which of the following is a universal constant?
5

70 calories of heat is required to raise the temperature of 2 moles of an ideal gas at constant pressure from 30°C to 35°C. The amount of heat required to raise the temperature of the same gas through the same range at constant volume is
6

The molar heat capacity for the process shown in the figure is
7

The molar heat capacity for the process shown in the figure is
8

In an isothermal process on an ideal gas, the pressure increases by 0.5%. The volume decreases by about
9

In an adiabatic process on gas with γ = 1.4, the pressure is increased by 0.5%. The volume decreases by about
10

Two samples A and B are initially kept in the same state. Sample A is expanded through an adiabatic process and sample B through an isothermal process. The final volumes of the samples are the same. The final pressures in A and B are pA and PB respectively.
11

Let Ta and Tb be the final temperatures of the samples A and B respectively in the previous question.
12

Let ΔWa and ΔWb be the work done by the systems A and B respectively in the previous question.
13

The molar heat capacity of oxygen gas at STP is nearly 2.5R. As the temperature is increased, it gradually increases and approaches 3.5R. The most appropriate reason for this behaviour is that at high temperatures.