A vessel containing one mole of a monatomic ideal gas (molecular weight = 20 g mol –1 ) is moving on a floor at a speed of 50 ms –1 . The vessel is stopped suddenly. Assuming that the mechanical energy lost has gone into the internal energy of the gas, find the rise in its temperature.

Question

Philoid · Accepted Answer

Given:

number of moles, n = 1

Specific heat at constant temperature, C_v(monoatomic gas) = 3R/2 = 12.471 J/mol/K

R = universal gas constant = 8.314 J/mol/K

Initial velocity(v_i) = 50 m/s

Final velocity(v_f) = 0

Molecular weight(m) = 20 g/mol = 0.02 kg/mol

Formula Used:

i. Change in internal energy(dU) = nC_vdT,

Where,

n is the number of the moles of the gas,

C_v is the heat capacity at the constant volume

dT = rise in temperature.

ii. Mechanical energy lost,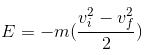

Where,

m is the molecular weight of the gas in kg

v_i is the initial velocity,

v_f is the final velocity,

equating equation (i) and (ii), we get

Putting the values in the above equation, we get

=> dT = rise in temperature ~ 2 K (Answer).

A vessel containing one mole of a monatomic ideal gas (molecular weight = 20 g mol–1) is moving on a floor at a speed of 50 ms–1. The vessel is stopped suddenly. Assuming that the mechanical energy lost has gone into the internal energy of the gas, find the rise in its temperature.

A vessel containing one mole of a monatomic ideal gas (molecular weight = 20 g mol^–1) is moving on a floor at a speed of 50 ms^–1. The vessel is stopped suddenly. Assuming that the mechanical energy lost has gone into the internal energy of the gas, find the rise in its temperature.