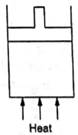
Figure shows a cylindrical container containing oxygen (γ = 1.4) and closed by a 50 kg frictionless piston. The area of cross section is 100 cm2, atmospheric pressure is 100 kPa and g is 10 ms–2. The cylinder is slowly heated for some time. Find the amount of heat supplied to the gas if the piston moves out through a distance of 20 cm.
Given:
Mass of piston(m) = 50 kg
Area(A) = 100 cm2 = (100x10-4)m2 (since 1m = 100 cm)
Acceleration due to gravity, g = 10 ms-2
Atmospheric pressure = 100 kPa
Distance through which it moves = 20 cm
γ = 1.4
Formula used:
Therefore, pressure exerted by piston = 
= 
= ((50x10)/(100x10-4)) Pa
= 50,000 Pa
Atmospheric pressure = 100 kPa = 1,00,000 Pa.
Therefore, Total pressure(P) = (50,000 + 1,00,000)Pa
=1,50,000Pa
Work done = Pressure x change in volume = P x dV
dV(change in volume) = distance moved by piston x Area
= (20cm x 100cm2)
= 2,000 cm3 = 2,000 x 10-6 m3 = 2 x 10-3 m3
Therefore, Work = (1,50,000 x 2 x 10-3) J = 300 J
Work done, W= P∆V =n R dT
We get,
Now, We calculate Q:
dQ= nCpdt =
Given: γ = 1.4 =
. Also,
. Solving these two equations, we get Cp = 7R/2, Cv = 5R/2.
Hence, dQ =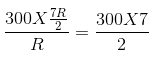 
= 1050 J.