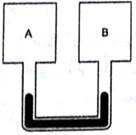
Figure shows two rigid vessels A and B, each of volume 200 cm3 containing an ideal gas (CV = 12.5 J K–1 mol–1). The vessels are connected to a manometer tube containing mercury. The pressure in both the vessels is 75 cm of mercury and the temperature is 300 K.
(a) Find the number of moles of the gas in each vessel.
(b) 5.0 J of heat is supplied to the gas in the vessel A and 10 J to the gas in the vessel B. Assuming no appreciable transfer of heat from A to B calculate the difference in the heights of mercury in the two sides of the manometer. Gas constant R = 8.3 J K–1 mol–1.
Given:
Gasses in both the vessels are at pressure of 75cm of mercury.
Therefore, 
The volume of the vessel is
The temperature of the gas is 300K
(a) For Ideal gasses,
where P,V and T are the pressure, volume and temperature of the gas, n is the number of moles, and R is the gas constant.
⇒ 
Therefore, number of moles = 0.008
(b) The specific heat of the gas at constant volume is CV = 12.5 J K–1 mol–1
Therefore, 
Where n is the number of moles, T is the rise in temperature, Q is the heat given.
Therefore, at constant volume, if we supply 5J and 10J heat to the vessels, the rise of temperature will be 
and 
So the change in pressure in the vessels will be governed by
So for the first vessel, Change in pressure
For the second vessel 
Therefore, the difference of pressure of the two vessels is
Which is equivalent to 
of mercury.
Therefore, the height of the mercury in the manometer tube is 12.5cm