Given:
Charge of the ring: Q
Radius of the ring :R
Let P be the point where electric field is found.
Distance between center of the ring and P is x.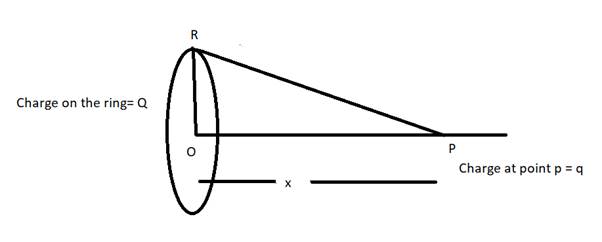

Formula used:
We know that electric field at any point on the axis at a distance x from the center is: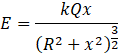
Where k is a constant and k= =9× 10⁹ Nm²C^-2. Q is the charge of the ring, x is the distance between center of the ring and point P and R is the radius of the ring.
Now for the electric field to be maximum, we use the maxima property:
Taking derivative of E w.r.t x,






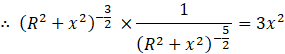
Hence Electric field is maximum at on the axis.