If the line segment joining the points P(x1, y1) and Q(x2, y2) subtends an angle α at the origin O, prove that : OP. OQ cos α = x1 x2 + y1 y2.

Key points to solve the problem:


• Idea of distance formula- Distance between two points P(x1,y1) and Q(x2,y2) is given by- PQ =


Given,


Two points P and Q subtends an angle α at the origin as shown in figure:



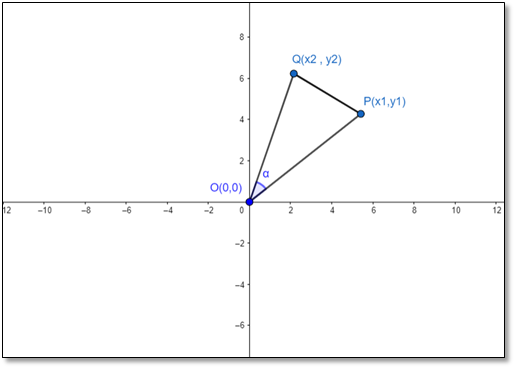
From figure we can see that points O,P and Q forms a triangle.


Clearly in ΔOPQ we have:


{from cosine formula in a triangle}


⇒ …..equation 1


From distance formula we have-


OP =


As, coordinates of O are (0, 0) ⇒ x2 = 0 and y2 = 0


Coordinates of P are (x1, y1) ⇒ x1 = x1 and y1 = y1


=


=


Similarly, OQ =


=


And, PQ =


∴ OP2 + OQ2 - PQ2 =


⇒ OP2 + OQ2 - PQ2 =


Using (a-b)2 = a2 + b2 – 2ab


∴ OP2 + OQ2 - PQ2 = 2x1 x2 + 2y1 y2 ….equation 2


From equation 1 and 2 we have:



⇒ …Proved.


1