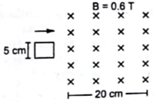
Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the emf induced in the loop at
(a) t = 2s, (b) t = 10 s
(c) t = 22 s, (d) t = 30s
Given:
Side length of square loop=5cm![]()
Speed of square loop![]()
Width of magnetic field ![]()
Magnetic field intensity =0.6T
(a) t=2s
distance moved by the loop![]()
area of the loop under magnetic field =
area of rectangle of length 0.05m and width 0.02m
![]()
Now,
Initial magnetic flux through the loop ![]() (at t=0)
(at t=0)
Final magnetic flux through the loop is given by
![]()
![]()
Average induced emf in time interval Δt is given by
![]() …(i)
…(i)
Where
![]() are flux across the cross section at time intervals
are flux across the cross section at time intervals ![]() respectively.
respectively.
Putting the values of ![]() in eqn.(i),
in eqn.(i),
![]()
Therefore magnitude of induced emf at t=2s is ![]()
(b) t=10s
distance moved by the square loop ![]()
at this moment, square loop is completely inside the magnetic field and area of loop through which flux pass ![]()
so the flux linkage does not changes with time ![]()
and thus from eqn.(i)
![]()
Therefore, magnitude of induced emf in the coil at t=10s is zero
(c) t=22s
distance moved by the loop ![]()
the loop is moving out of the field, the area of loop under the field is ![]()
the magnetic flux acting on the loop is
![]()
(- sign as the flux has decreased)
The induced emf is
![]()
Therefore magnitude of induced emf at t=22s is ![]()
(d) t=30s
distance moved by the square loop![]()
at this time, square loop is completely outside the magnetic field and the area of loo through which flux passes =0
hence the flux linkage through the loop remains zero ![]()
and thus from eqn.(i)
![]()