A circular coil of radius 2.00 cm has 50 turns. A uniform magnetic field B = 0.200 T exists in the space in a direction parallel to the axis of the loop. The coil is now rotated about a diameter through an angle of 60.0°. The operation takes 0.100s. (a) Find the average emf induced in the coil. (b) If the coil is a closed one (with the two ends joined together) and has a resistance of 4.00 Ω, calculate the net charge crossing a cross-section of the wire of the coil.

Question

Philoid · Accepted Answer

Given:

Radius of coil

No. of turns in the coil

Magnetic field intensity

We know that,

Flux (ϕ) of magnetic field (B) through the loop of cross section area A in the magnetic field is given by

Where N=no. of turns in the coil

Since magnetic field is perpendicular to the loop the flux becomes

Initial flux through the coil is given by

After 0.1 s the coil is rotated through an angle of 60° =θ

Finally, the flux through the coil becomes

Average induced emf in time interval Δt is given by

…(i)

Where

are flux across the cross section at time intervals respectively.

Using eqn.(i) emf induced in the coil is given by

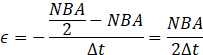
Putting the values of N, B, A and Δt in above eqn. we get

Therefore average emf induced in the coil is

(b) the current through the coil (i) is calculated using formula

Hence the charge(Q) crossing the cross-section of the wire in time interval Δt is

Putting the values of ϵ, R and Δt we get,

Therefore charge crossing cross-section of the wire in the coil is