The rectangular wire-frame, shown in figure has a width d, mass m, resistance R and a large length. A uniform magnetic field B exists to the left of the frame. A constant force F starts pushing the frame into the magnetic field at t =0.
(a) Find the acceleration of the frame when its speed has increased to v.
(b) Show that after some time the frame will move with a constant velocity till the whole frame enters into the magnetic field. Find this velocity v0.
(c) Show that the velocity at time t is given by
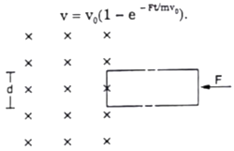
Given:
Length of sliding wire = width of frame = d
Mass = m
Resistance = R
Magnetic field = B
Initial force = F
Formula used:
(a) Induced emf(when it attains a speed v) 
… (i), where B = magnetic field, d = width of frame, v = velocity
Therefore, induced current 
, where E = induced emf, R = resistance ⇒ 
… (ii)
Now, magnetic force acting on the wire 
… (iii), where I = current, d = length of sliding wire = width of frame, B = magnetic field
Substituting (ii) in (iii), 
… (iv)
Now, as the magnetic force is in opposite direction to applied force, net force = 
… (v)
But, from Newton’s 2nd law of motion, net force = ma … (vi), where m = mass, a = acceleration
Equating (v) and (vi):
⇒ 
Acceleration of the frame at speed 
(Ans)
(b) For the velocity to be constant, acceleration needs to be 0.
Hence, from previous part,
where F = external force, m = mass, B = magnetic field, d = width of frame, v0 = constant velocity, R = resistance
=> 
Constant velocity 
(Ans)
(c) From part (a), acceleration 
Now, acceleration a = dv/dt, where v= velocity, t = time
Hence, 
=>
Integrating with proper limits, we get
=>
>
=>
=>
=>
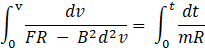
But, from previous part (b), we found out that 
⇒
Hence,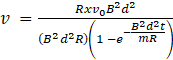 
=> 
(proved)