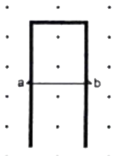
A conducting wire ab of length ℓ, resistance r and mass m starts sliding at t = 0 down a smooth, vertical, thick pair of connected rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails.
(a) Write the induced emf in the loop at an instant t when the speed of the wire is v.
(b) What would be the magnitude and direction of the induced current in the wire?
(c) Find the downward acceleration of the wire at this instant.
(d) After sufficient time, the wire starts moving with a constant velocity. Find this velocity vm.
(e) Find the velocity of the wire as a function of time.
(f) Find the displacement of the wire as a function of time.
(g) Show that the rate of heat developed in the wire is equal to the rate at which the gravitational potential energy is decreased after steady state is reached.
Given:
Length of sliding wire ab = l
Resistance = r
Mass = m
Magnetic field = B
Speed = v
Formula used:
(a) Induced emf in the loop 
(Ans), where B = magnetic field, l = length, v = velocity
(b) Induced current in the wire 
= 
(Ans) , where E = emf, r = resistance
As the wire is moving, the magnetic flux is increasing. Hence, the direction of the current will be such as to oppose the increase in flux. Hence, the current will move from b to a.
(c) Magnetic force on the wire(upward) 
… (i), where I = current, l = length of sliding wire, B = magnetic field.
Weight acting downward = mg
Hence, net downward force = 
… (ii)
According to Newton’s 2nd law of motion, net force = ma … (iii), where m = mass, a = acceleration.
Hence, equating (ii) and (iii), 
But, I = E/r, where I = current, E = emf, r = resistance => I = Blv/r, where B = magnetic field, l = length of sliding wire, v = velocity
=> acceleration 
(Ans)
(d) When the wire will move with constant velocity (let it be v0), acceleration will be 0.
Hence, from part (d) of this question,
= 0
=> constant velocity 
(Ans)
(e) From part (c),
But, a = dv/dt, where v = velocity, t = time
Therefore, 
⇒ 
Integrating with proper limits, we get
⇒
>
⇒
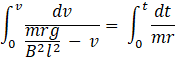
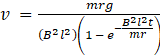
But, from the previous part,
Therefore, velocity as a function of time : 
(Ans)
(f) Now, v can be written as dx/dt, where x = position, t = time
Therefore, from previous part, 
=>
Integrating with suitable limits, we get:
=>
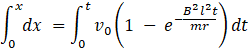
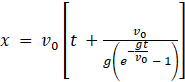
=> Displacement as a function of time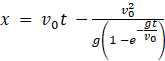 
(Ans)
(g) Then, 
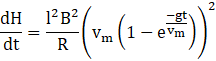
After steady state, 
Hence after steady state,
So, the rate of heat developed in the wire is equal to the rate at which the gravitational potential energy is decreased after steady state is reached.