Figure shows a square frame of wire having a total resistance r placed co-planarly with long, straight wire. The wire carries a current I given by i = i0 sin ωt. Find
(a) the flux of the magnetic field through the square frame,
(b) the emf induced in the frame and
(c) the heat developed in the frame in the time interval 0 to 
.
Given:
Current in wire i = i0 sin ωt
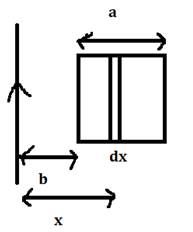
Length of each side of square loop = a
Distance of one edge from wire = b
Diagram:
Formula used:
Magnetic flux 
… (i), where 
= magnetic flux, B = magnetic field, da = area element
Magnetic field due to a long current carrying wire at distance x 
… (ii), where μ0 = magnetic permeability of vacuum, i = current, x = distance from wire
We consider a strip of width dx at a distance x from the wire.
Now, area element da = a dx, where a = length of loop, dx = width element
Hence, from (i) and (ii),
Flux 
(ans)
(b) Emf induced in frame 
where 
= flux, t = time
From previous part, 
re, 
⇒ 
= 
(Ans)
(c)Heat developed in wire
, where i = current through frame, r = resistance, t = time
From previous i = E/r = 
where E = emf, r = resistance
Hence H = 
Now, Given: 
Hence, H = 