Given

The reaction given in this scenario is

The number of nuclei = 1000, the initial time taken = 0, the number of at time, half-life of and half-life of. Hence, to find the value of time t when it is maximum, we use the relation of decay rate and number of live atom with respect to time.

Formula used

According to the Radioactive Decay Law or Rutherford Soddy Law the decay rate of a nucleus is given by the formula of

,

where

is the rate of decay of the nucleus with respect to time, is the decay rate constant of the nucleus and N is the number of active nuclei.

Explanation

The radioactive decay of Sulphur and Chlorine is given as

The number of active Sulphur nuclei

The decay rate constant of Sulphur

The number of active Chlorine nuclei

The decay rate constant of Chlorine

With the formula of radioactive decay in terms of initial and final number of atoms both before and after decay is

The rate of decay of active number of nuclei of Chlorine is

_______________ (1)

Multiplying on both sides and integrating we get the sides as

______________ (2)

Now since at time, the number of chlorine nuclei () = 0. Therefore, the equation now stands as

The value of C = -

Hence, putting the value of C in equation (2) we get:

______________ (3)

To find the maximize value of the chlorine, we integrate the equation (3) on both side with respect to time and putting, we get

Integrating, the above equation to find the value of t in terms of which leads to the time, when the number of nuclei is maximum

_____________________ (4)

Now to find the value of time t, we put the value of in equation (4),

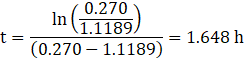
Therefore, the time at which the value of active nuclei of Chlorine will be maximum is 1.648 h.