A wire of length ℓ is bent in the form of an equilateral triangle and carries an electric current i. (a) Find the magnetic field B at the centre.
(b) If the wire is bent in the form of a square, what would be the value of B at the centre?
(a)
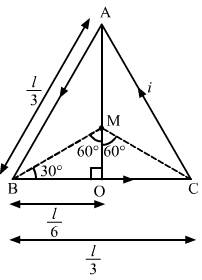
Let M be the midpoint of equilateral ΔABC
∴ ![]()
current is given to be i
Hence, in ΔAOB
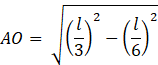
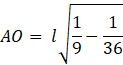
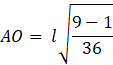
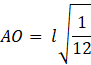
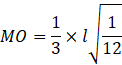
![]()
The angles made by points B and C with centre M are ![]() respectively,
respectively,
Hence separation of the point from the wire is given by, ![]()
Thus, the magnetic field induced due to current in wire BC is-
![]()
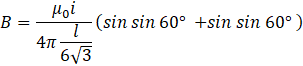
![]()
Now,
Net magnetic field at point M is given as Magnetic field due to wire BC + Magnetic field due to wire CA + Magnetic field due to wire AB
Since all wires are equal,
![]()
It is perpendicular to the plane in outward direction if current is anticlockwise and in an inward direction if the current is clockwise.
(b)
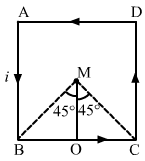
The angles made by B and C with centre M are ![]()
Distance between point from the wire, ![]()
Thus, the induced magnetic field due to electric current in wire BC is given by
![]()
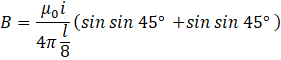
![]()
Since all wires are equal,
Net magnetic field at point M = 4 × Magnetic field due to wire BC
![]()