We have to find the resistance associated with the truncated cone as shown in the figure.

For that purpose, we take an elemental area of this uniformly increasing cone and find the resistance of that element. By integrating that value from radius a to b, we would be able to find the resistance associated with the truncated cone.

The expression for the resistance, R, of a cylinder with length ‘l’ and area of cross-section A is,

We assume that the cone is made up of an infinite number of cylinders with length ‘dx’.

So for that element, resistance dR is

Hence the total resistance R is

Now the resistance for an element with a radius ‘y’ at x distance from left with length ‘dx’ should be found out.

The mean area of the element is,

Hence eqn.1 becomes

From the figure, we can write a relation connecting x and y as,

Or,

Differentiating the above expression, we get,

On re-arranging

Substituting this value in eqn.1 and combining with eqn.3, we get,

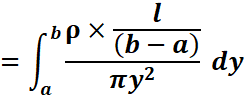
On integration,

Or,

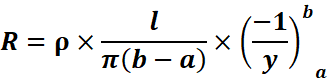
Or,

Or,

Hence the resistance of the truncated cone is