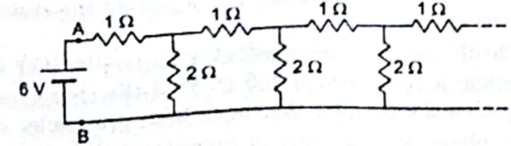
An infinite ladder is constructed with 1Ω and 2Ω resistors as shown in figure.
(a) Find the effective resistance between the points A and B.
(b) Find the current that passes through the 2Ω resistor nearest to the battery.
Concepts/Formula used:
Resistors in Series:
![]()
Resistors in parallel:
![]()
Ohm’s Law:
Potential Difference (V) across a resistor of resistance R when current I passes through it is given by Ohm’s law:
![]()
(a)
Let the equivalent resistance between A and B be req Ω .
This means that we can rewrite the circuit as:
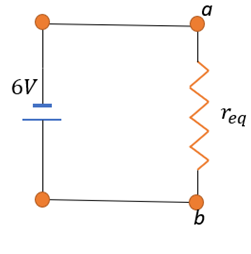
Where req has replaced the following infinite combination:
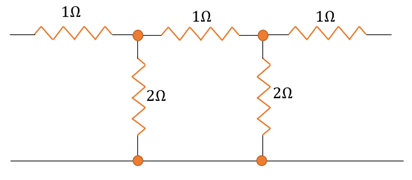
We can redraw the infinite circuit as
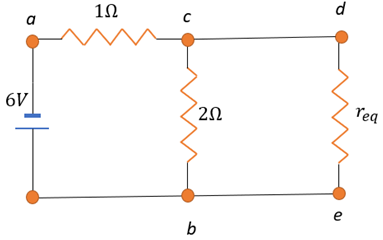
Note that de and cb are in parallel. The equivalent resistance is given by:
![]()
![]()
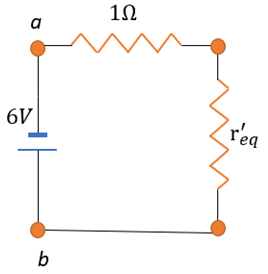
Now, the 1 Ω resistor and r’eq are in series.
![]()
![]()
Rearranging and dropping the subscript, we get a quadratic equation:
![]()
The roots of this equation are 2 and -1. As resistance can’t the negative the equivalent resistance between A and B is 2 Ω.
(b)
Let the net current be 2I. This current passes through the 1 Ω resistor. Than splits up equally due to symmetry as there are two 2Ω resistors.
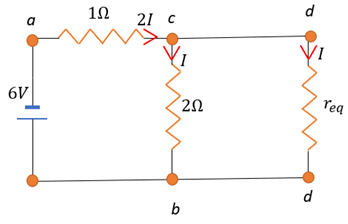
Now,
![]()
![]()
Hence, the current passing through the nearest 2 Ω resistor is 1.5A.