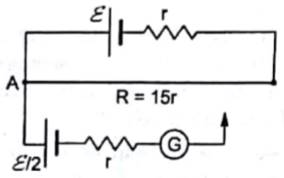
Consider the potentiometer circuit arranged as in figure. The potentiometer wire is 600 cm long.
(a) At what distance from the point A should the jockey touch the wire to get zero deflection in the galvanometer?
(b) If the jockey touches the wire at a distance of 560 cm from A, what will be the current in the galvanometer?
Concepts/Formula used:
Ohm’s Law:
Potential Difference (V) across a resistor of resistance R when current I passes through it is given by Ohm’s law:
![]()
Let the area of cross section of the wire (resistor) be A and resistivity be ρ.
Then,
![]()
Kirchhoff’s loop rule:
The sum of potential differences around a closed loop is zero.
(a)
We consider the circuit when there is no deflection:
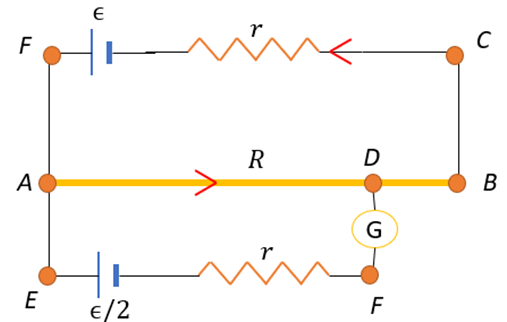
Applying Kirchhoff’s rule on loop ABCF,
![]()
![]()
Using ![]() ,
,
![]()
![]()
![]()
![]()
Let the area of cross section of wire be A and resistivity be ρ.
Then,
![]()
where V is the voltage across a wire segment of length l.
As, all the quantities except for length are the same for all sections of wire AB,
![]()
Hence,
![]()
![]()
![]()
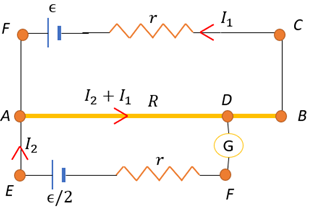
(b)
Let the current coming out of the main battery be I1 and the current through the galvanometer be I2.
Let the area of cross section of wire be A and resistivity be ρ.
Then,
![]()
where V is the voltage across a wire segment of length l.
As, all the quantities except for length are the same for all sections of wire AB,
![]()
Hence,
![]()
Using ![]()
![]()
Now, RAD and RDB are in series.
![]()
![]()
![]()
Applying Kirchhoff’s rule on loop ABCFA,
![]()
![]()
![]() ……………(1)
……………(1)
Applying Kirchhoff’s rule on loop ADEFA,
![]()
![]()
![]() ………………(2)
………………(2)
From (i) and (ii)
![]()