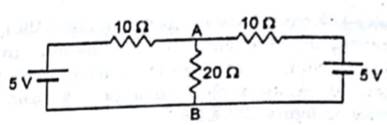
(a) Find the current in the 20 Ω resistor shown in figure.
(b) If a capacitor of capacitance 4 μF is joined between the points A and B, what would be the electrostatic energy stored in it in steady state?
Concepts/Formula used:
Ohm’s Law:
Potential Difference (V) across a resistor of resistance R when current I passes through it is given by Ohm’s law:
![]()
Kirchhoff’s junction rule:
The sum of currents entering a junction is equal to the sum of currents leaving it.
Kirchhoff’s loop rule:
The sum of potential differences around a closed loop is zero.
Energy stored by a capacitor:
If the potential difference between the two conductors of the capacitor is V and its capacitance is C, its energy is given by:![]()
(a)
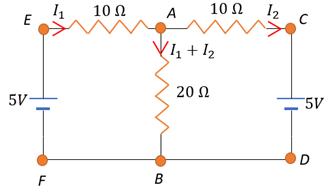
Using Kirchhoff’s law on loop FEABF,
![]()
![]()
![]() ........(1)
........(1)
Using Kirchhoff’s law on loop ACDBA,
![]()
![]()
![]() ……………(2)
……………(2)
Solving (1) and (2), we get
![]()
Hence,
![]()
(b)
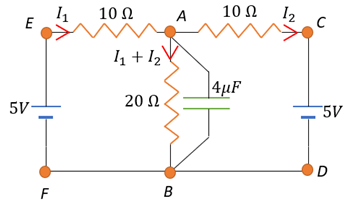
At steady state, no current passes through the capacitor; hence, the results are the same as in (a).
![]()
Now, the potential as the capacitor is in parallel with the 20Ω resistor,
![]()
![]()
![]()
![]()
Hence, the energy stored by the capacitor is 32μJ.