In the arrangement shown in figure (3-Q3), the ends P and Q of an inextensible string move downwards with uniform speed u. Pulleys A and B are fixed. The mass M moves upwards with a speed
Let 
be the length of the string from the mass to the pulley. Let 
be the length of the string from the mass to the rigid body and 
be the constant. This is shown in the figure below:
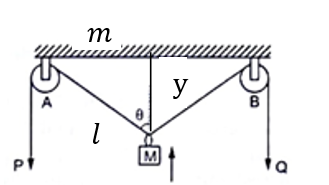
The string through the pulley has velocity 
along 
while the mass/string has velocity 
along 
.
By Pythagoras theorem in triangle formed in above figure, we have
Differentiating above equation with respect to time, we get
Negative sign is due to the fact that the 
and 
decreases as time goes.
Therefore, the equation (1) becomes
The equation above gives the velocity of the mass.
1