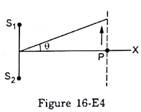
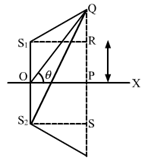
Two speakers S1 and S2, driven by the same amplifier, are placed at y = 1.0 m and y = - 1.0 m (figure 16-E4). The speakers vibrate in phase at 600 Hz. A man stands at a point on the X-axis at a very large distance from the origin and starts moving parallel to the Y-axis. The speed of sound in air is 330 m/s. (a) At what angle θ will the intensity of sound drop to a minimum for the first time? (b) At what angle will he hear a maximum of sound intensity for the first time? (C) If he continues to walk along the line, how many more maxima can he hear?
Given:
Frequency of source 
Speed of sound in air
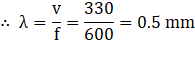
Let the man travel a distance of 
parallel to the y-axis and let 
be the distance between the two speakers. The man is standing at a distance of 
from the origin.
The path difference 
between the two sound waves reaching the man is given by:
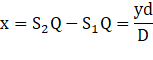
Angle made by man with the origin:
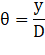
Given:
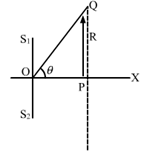
(a) For minimum intensity:
The destructive interference of sound (minimum intensity) takes place if the path difference is an odd integral multiple of half of the wavelength.
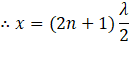
For (n=0)
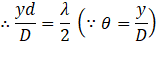
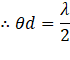
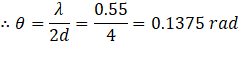
(a) For maximum intensity:
The constructive interference of sound (maximum intensity) takes place if the path difference is an integral multiple of the wavelength.
For (n=1):
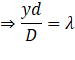
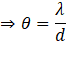
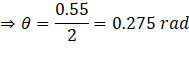
(c) The more number of maxima is given by the path difference:
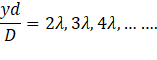
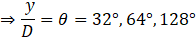
He will hear two more maxima at 
and 
because the maximum value of 
may be
.