A car is going at a speed of 21.6 km/hr when it encounters a 12.8 m long slope of angle 30o (figure 6-E5). The friction coefficient between the road and the tyre is 1/2√3. Show that no matter how hard the driver applies the brakes; the car will reach the bottom with a speed greater than 36 km/hr. Take g = 10 m/s2.
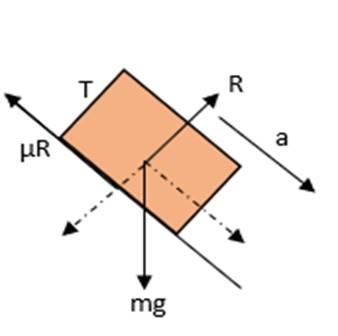
The maximum force of friction is developed between the surface of road and the car’s tyres when hard breaks are applied.
So, maximum frictional force = μR
From the free body diagram,
R − mg cos θ = 0
⇒ R = mg cos θ (i)
and
μR + ma − mg sin θ = 0 (ii)
⇒ μ mg cos θ + ma − mg sin θ = 0
⇒ μg cos θ + a -10(12) =0
⇒ a=5- {1-(2![]() )} ×10(
)} ×10(![]() /2)
/2)
⇒ a = -2.5 m/s2
When brakes are applied, car will deaccelerate by 2.5 m/s2
Distance s= 12.8 m
initial velocity u = 6 m/s
∴ Velocity at the end of incline
ν=![]()
![]()
v=10 m/s=36 km/h
Hence, the harder the driver applies the brakes, the lower will be the velocity of the car when it reaches the ground, i.e. at 36 km/h