Consider a circular current-carrying loop of radius R in the x-y plane with center at origin. Consider the line integral taken along z-axis. (a) Show that monotonically increases with L. (b) Use an appropriate Amperian loop to show that .

Question

Philoid · Accepted Answer

Now from the diagram

L=R tanθ

Putting it back to the equation,

eq.1

a) As sinθ always increases from 0 to π/2. Hence is also monotonically increasing function.

b)

When

So,

c)From eq1.

Now

So,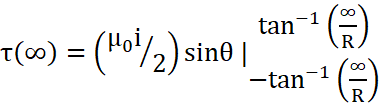

,

d) _circular> _square.

We can further find _square using the magnetic induction due to a wire.

But as there is no term representing the characteristics of the loop in .

So it remains the same.

Consider a circular current-carrying loop of radius R in the x-y plane with center at origin. Consider the line integral taken along z-axis.(a) Show that monotonically increases with L.(b) Use an appropriate Amperian loop to show that .

Consider a circular current-carrying loop of radius R in the x-y plane with center at origin. Consider the line integral
taken along z-axis.

(a) Show that monotonically increases with L.

(b) Use an appropriate Amperian loop to show that .